分汤

808. 分汤 - 力扣

---

题型描述

二维概率DP

数据范围小时DP，范围大时为特定值

题目描述&数据范围

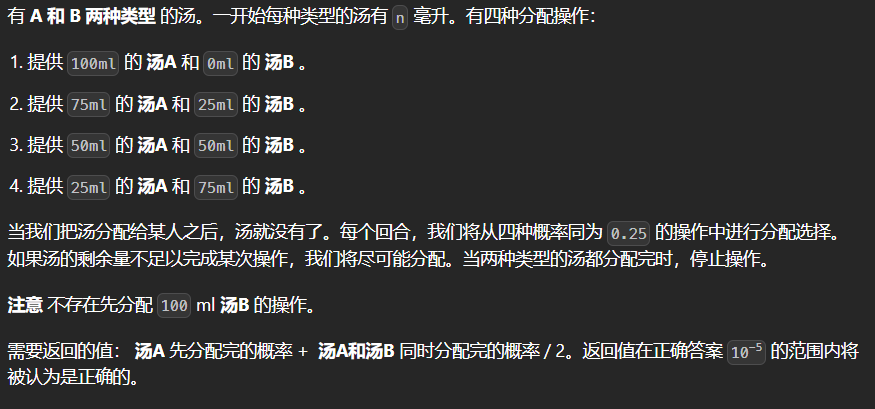
$1\leq n\leq 10^9$

题解

数据较小的时候可以DP

由于以 $25$ 为分汤单位，所以可以整体除 $25$

设 $dp[i][j]$ 表示 $A,B$ 分别有 $i,j$ 份时的答案

显然边界条件为：
$$
dp[i][j]=
\begin{cases}
0 & (i>0,j=0)\\
0.5 & (i=0,j=0)\\
1 & (i=0,j>0)\\
\end{cases}
$$
转移方程：
$$
dp[i][j]=\frac{1}{4}(dp[i-4][j-0]+dp[i-3][j-1]+dp[i-2][j-2]+dp[i-1][j-3])
$$

代码

double dp[200][200];
    double soupServings(int n) {
	    n=ceil(n*1.0/25);
	    if(n>200){return 1;}
	    for(int i=1;i<=n;++i){
            dp[i][0]=0;
            dp[0][i]=1;
        }
        dp[0][0]=0.5;
        for(int i=1;i<=n;++i){
            for(int j=1;j<=n;++j){
                dp[i][j]=0.25*(dp[max(i-4,0)][j]+dp[max(i-3,0)][max(j-1,0)]+dp[max(i-2,0)][max(j-2,0)]+dp[max(i-1,0)][max(j-3,0)]);
            }
        }
        return dp[n][n];
    }